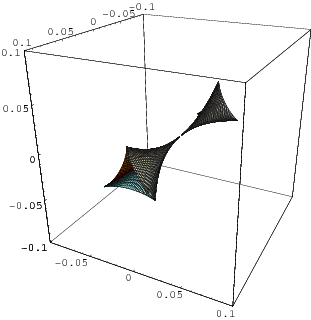
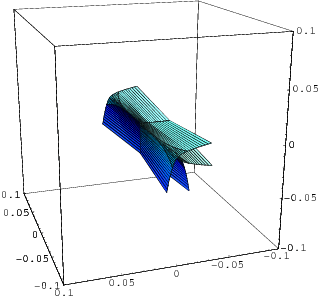
In case you were wondering, diagram 1A represents the Elliptic Umbilic Catastrophe which has the equation
, and diagram 1B represents the Hyperbolic Umbilic Catastrophe he hyperbolic umbilic is the universal unfolding of the function germ 
. Catastrophes as applied to calculus and analysis are bifurcations between different equilibria, or fixed point attractors. Due to their restricted nature, catastrophes can be classified based on how many control parameters are being simulataneously varied. For example, if there are two controls, then one finds the most common type, called a "cusp" catastrophe. If, however, there are move than five controls, there is no classification.
Catastrophe theory studies and classifies phenomena characterized by sudden shifts in behavior arising from small changes in circumstances, and is an offshoot of dynamical systems theory, which allows mathematicians and scientists to study the behavior of many types of systems spanning various branches of science within a unified framework. This is all very closely related to chaos theory, where it gets either unbelievably complicated or just silly depending on how you look at it.
(bifuraction)
(when mathematicians go crazy with the paintbox)
That's all for now, stay tuned for the second installation of math-magic
|